Reinforcement Learning Course 1 Week 3
Notes for Reinforcement Learning Course 1 Week 3.
TLDR
- Introduction to Policies
- Evaluation of the Policies
Prerequisites
The previous blog, Reinforcement learning specialization, Course 1, week 2.
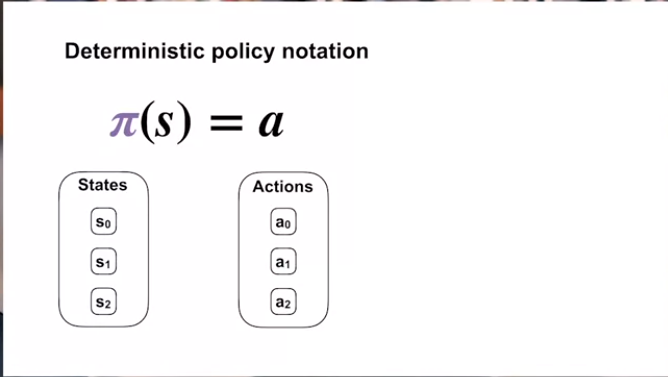
Policies!
So what is a policy? Simply put whatever action is taken by the agent in a certain state. For example, if the day (state) is Monday, I will have to go to work. If the day is Saturday, I will sleep. We can formulate,
$\pi (S_{day}=Monday) = {Work} $
$\pi (S_{day}=Saturday) = {Sleep} $
This can be shown as
For our example, we can say,
| State ($s$) | Action ($a = \pi (s)$) |
|---|---|
| Monday | Work |
| Saturday | Sleep |
But this does not take into account the fact of randomness!
In the above example, our action per state is fixed. On Mondays, zero-chance of sleeping. On Saturday zero chance of working! We will call it the Deterministic Policy. But in real life, this might not always be the case!! On some Mondays we may take paid leaves and sleep all day. On some Saturdays, we might need to work due to the deadline! May and /or Might means there is a function of probability!
We can write like
| State ($s$) | Action ($a = \pi (s) = P(action|state)$) |
|---|---|
| Monday | P(action=work|state)=$0.9$ |
| Saturday | P(action=sleep|state)=$0.9$ |
This is not 100% accurate, but you will get the idea. This policy is known as the Stochastic Policy.
The stochastic policy is shown as $\pi (a |s)$ meaning the probability of action $a$ over the state $s$.
Because it is a probability, then it must follow two rules,
$ \sum \pi (a |s) = 1 $
and
$ \pi (a | s) \geq 0 $
Value Function
Let us go back to our weekday-work-weekend-sleep example. For Monday we will work, and for Saturday we will sleep. What about Sunday and Friday? I do not know about others. What happens to me is that I start to get sleepy on Fridays! Because I keep thinking, Saturday is coming! On the other hand, on Sundays, I start to get prepared for work!
| State ($s$) | Action ($a = \pi (s) = P(action|state)$) |
|---|---|
| Monday | P(action=work|state)=$0.9$ |
| Friday | P(action=sleep|state)=$0.4$ , P(action=work|state) = $0.6$ |
| Saturday | P(action=sleep|state)=$0.9$ |
| Sunday | P(action=sleep|state)=$0.6$, P(action=work|state) = $0.4$ |
Here we can call the Monday starting state, and the Saturday as terminal state (for now.) The states closer to the starting and terminal states are affected by the respective terminal states, right? This phenomenon can be expressed using the value function!
Let’s evaluate the days
Clearly from our example, we can see not all days have the same values to us. Depending on the closeness of the states to the goals/rewards/terminations, we can simply add another parameter to the state other than the reward, $value$. The functions to determine the state’s values are called as $value$ function!
Now, the getting - or not getting - the rewards do not only depend on the state. It should also depend on our actions! Suppose you did not work on Thursday, but you have a deadline! So you have to ditch sleep on Friday and work more! This affects the next state! We can call them action value! And the function to determine the action values? Action value functions!! More on the later blogs about how to determine the Action value functions!
Reference
- All of the screenshots are from Course 1, Week 3 of the Reinforcement Learning Specialization.