Reinforcement Learning Course 2 Week 1

Notes for Reinforcement Learning Course 2 Week 2.

TLDR

• Monte Carlo method definition
• Exploration vs Exploitation
• Exploring start policy vs Soft epsilon policyß

Monte Carlo method

In the previous course, we learned about the dynamic programming method. This method requires the dynamics of the environment. What if we do not or cannot have the dynamics of the environment? What if we have large random samples of the environment? In this case, the Monte Carlo method comes to the rescue.

What is the Monte Carlo method?

Simple. For a certain state, $s$ , we take random samples of the returns $(r^s_0, r^s_1, r^s_2, r^s_3…r^s_n)$. We will average $ \begin{equation} v^s_{\pi} = \frac{\sum^n_{i=0} r_i}{n} \end{equation} $

Simple, right?

Real life intuition!

The above photo is taken from pexels[dot]com.

In real life (IRL), how do we learn everything? Just think about it. For example Football (Americans call it Soccer, but it is Real football!). How do you learn to play the game of football? Do you try to understand the physics of football? For example, if you are taking a penalty kick there are two options for you to learn how to take an optimum penalty kick.

a) You start learning the physics of penalty kick. That means you have to study the aerodynamics of the ball, the environment that day, and the state of the Goalkeeper, and maybe then you can calculate the exact force and direction by which you have to hit the ball!

b) OR, you start practicing with the ball every day!

I think we all know the answer. WE DO NOT GO FOR (a)! Not only is this close to impossible, but even if it was possible, it would take ALL THE FUN THERE ARE IN A GAME! Anyway, (a) is Dynamic programming, and (b) is Monte Carlo learning. Actually, very close to it! But you get the big idea, right?

Here is what is happening,

When you are taking thousands of shots you are collecting the “sample states” -> $s_t$

Kicking the ball is action -> $a_t$

You may score a goal or not. They can be rewarded $r_t$.

The most important part, your brain learns to kick the ball in the right force and direction by collecting the samples!!

Exploration

For the Monte Carlo method, as the agent does not have full knowledge of the dynamics of the environment and it is basically a sampling-based method, it is necessary to give the agent as much information as possible about different states.

Let’s get back to the penalty kick situation

Suppose you are a goalkeeper, You want to train yourself as much as possible. You are never able to know the physics of all football matches. Even if you do, by the time you can calculate the position of the penalty taker, it’s already the goal! So what should you do? Like I said, practice!!! The more different types of goal-stopping practice you can do, the more probability of stopping the goals in the real matches!! These different scenarios of shooting practice are samples. The more diverse the samples are the better the chances of training yourself for the games or in other words “generalizing” the agent! This is exactly what exploration does!

Exploration in the environments!

So! We have got an idea about the need for exploration! How to do it in an RL environment? There are two popular ways to do so!

Exploring start policy

In this case, the agent will start at a random initial state every time it starts playing the game. This way the agent should start learning to generalize. For example, if you play chess, you are always starting from the same initial state. How about we randomize your initialize your state every time?! Sometimes you might be just before an obvious checkmate, sometimes you might be check-mated! Either way, you will learn to train yourself in all sorts of initial positions! But it has a problem. It only deals with random initial states! It does not directly affect the behavior of the agent as per the policy! For example, back to chess, if you always follow a certain policy for chess, No matter what the initial state is, your policy might not be affected.

Epsilon-soft policy

In this case, the agent will choose random action based on a threshold $\epsilon$, which is why this policy is named $\epsilon$ -soft policy. The biggest advantage is that the agent will learn about the value of a state and action at any state at any time. This policy has more chance of training the agent with all of the available state spaces.

Going back to our Football (aka Soccer) intuition, it is more like trying different types of shots at different places of the D-box! Sometimes you try the working action or / shots, sometimes you experiment in practice!

The algorithm for epsilon-soft policy is as follows

Off-policy learning

What is off-policy learning?

Till now, we were assuming that the agent that will interact with the environment is the same agent we will train every time it interacts (also known as an episode). This is known as on-policy learning. What if we have two agents? One for learning and one for explore - exploit? It is playing an online First-person shooter game in a team. You explore some places and let others know about your observations. They will use this knowledge (or dare I say training) in the other periods (or episodes) of the game!

Why is it important?

The problem of the exploration-exploitation dilemma stems from the fact that the same agent has to explore sometimes and it has to exploit sometimes. Using two policies, one which only explores (let’s call it behavior policy $b(a|s)$) and the other policy is the policy which will only be used to exploit (i.e. use the training from the exploration to get the best action; let’s call it target policy $\pi(a|s)$). This way the agent can learn from the exploration and exploit the knowledge in future episodes. This way we can use the best of both worlds! The behavior policy will help our agent to learn all possible actions for every state (at least most of the states!) and the target policy will help the agent to take the best action! The below picture shows two types of policies. Can you guess which one is the behavior policy and which one is the target policy? 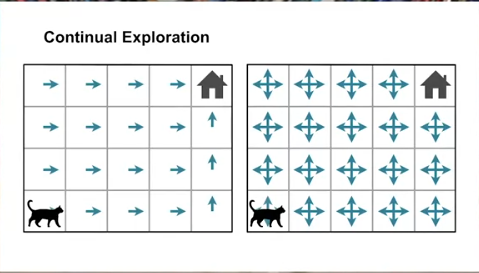Source : [2]

Now here is an issue with off policy See when we are exploring, we are using a policy named $\pi_b$, the policy we want to evaluate and improve is $\pi_t$. Recall the equation for the expected rewards for a policy.

$ \begin{equation} E(\pi | s) = \sum \pi G^{T}_{t=0} \end{equation} $

The expected rewards we get for behavior policy $G_{\pi_b}$ will be by definition different than that of target policy $G_{\pi_t}$. But how can we get the correct expected reward?

Importance sampling

Let me be honest! I have no idea how to make a real-life intuition for this concept!!! All of the videos I have watched are technical!!! So this is the only way I can explain! If any reader can provide intuition, please do so!

Here is a statistical trick! Let’s assume there is a variable $x$ and there are two functions $f(x)$ and $g(x)$. We want to calculate the expected value of $f(x)$ which is $E(f(x))= \sum xf(x)$ based on the distribution of $g(x)$. We can do this by the following equation.

$ \begin{equation} E(f(x)) = \sum_{i=0}^{i=N} x_i f(x_i) \end{equation} $ $ \begin{equation} E(f) = \sum_{i=0}^{i=N} x_i \frac{f(x_i)}{g(x_i)} g(x_i) \end{equation} $ $ \begin{equation} E(f) = \sum_{i=0}^{i=N} \rho_(x_i) x_i g(x_i) \end{equation} $

How will we get the value of $\sum_{i=0}^{i=N} x_i g(x_i) $ ? This is THE TRICK!

$ \begin{equation} \sum_{i=0}^{i=N} x_i g(x_i) \approx \frac{1}{N} \sum_{i=0}^{i=N} x_i \end{equation} $

where the parameter named importance ratio $\rho$ such as

$ \begin{equation} \rho (x_i) = \frac{f(x_i)}{g(x_i)} \end{equation} $

Or we can say

$ \begin{equation} E(f) \approx \frac{1}{N} \sum_{i=0}^{i=N} x_i \rho_(x_i) \end{equation} $

What are we doing?!

In statistics, this is called the importance sampling. The theory is as follows if we have two distributions $f(x)$ and $g(x)$ where we can only get the values of $g(x)$ not the $f(x)$ for whatever reason or if it is very hard to sample from $f(x)$, then in that case, the expected value of $f(x)$ is approximately the multiplication of the importance sampling ratio $\rho$ and the average of $x_i$ under the distribution of $f(x) \bigcap g(x)$. Now this area of $f(x)$ and $g(x)$ is the area where we can sample from both distributions. That is why it is important to have a good sampling of the area. For more details please refer to the video [3].

The above equation tells us this important information! When we know the importance sampling ratio we can easily get the expected reward for the target policy based on that of behavior policy!!!

but how can we get the Expected rewards for the behavior policy?

Well, we already know that don’t we?

In our case, the equation will be like this. $ \begin{equation} E(\pi_t(s)) \approx \sum \rho s \pi_b (s) \end{equation} $

Reference

[1] The images used in this article are downloaded from pexels dot com.

[2] Coursera Sample-based learning methods video on off policy.

[3] Importance sampling video by Mathematicalmonk link